Práctica #2.
Nombre de la práctica: Implementación de funciones lógicas usando compuertas.
Nombre: David Santiago Martínez Molina
Código: 20181005164
Asignatura: Fundamentos de circuitos digitales
Programa : Ingeniería Electrónica
Docente : César Andrey Perdomo Charry
INTRODUCCIÓN:
Durante este informe se evidenciará el desarrollo de la práctica #2. Como sabemos, los circuitos lógicos realizan operaciones a través de señales digitales y casi siempre se implementan como circuitos. Electrónicamente, el valor de la señal está limitado a algunos valores discretos. En un circuito lógico binario, solo hay dos valores: 0 y 1. Como resultado, los circuitos lógicos digitales pueden analizarse y diseñarse funcionalmente utilizando álgebra de conmutación, tablas de verdad y otros medios para describir el funcionamiento de ceros y unos en un circuito. Se puede decir que un sistema digital combinacional es aquel sistema en el que las salidas son solamente función de las entradas actuales, es decir, dependen únicamente de las combinaciones de las entradas(Figura 1).
Figura 1. Ejemplo circuito lógico.
Entonces, la relación entre las variables de entrada y salida se pueden representar mediante una tabla de verdad. Podemos definir una tabla de verdad como una forma de representación de una función en la que se indica el valor 0 o 1 para cada valor que toma ésta por cada una de las posibles combinaciones que las variables de entrada pueden tomar. (El número total de combinaciones es 2^n , siendo n el número de las entradas).
Figura 2. Tabla de verdad.
Como hemos visto , las puertas lógicas fundamentales son tres (AND, OR y NOR) y haciendo la combinación de algunas de las puertas anteriores podemos obtener otras nuevas (NAND, NOR, XOR, ....). Estas compuertas se pueden definir de la siguiente manera: la compuerta AND genera una salida 1 si y sólo si todas sus entradas son 1, una compuerta OR produce una salida 1 si y sólo si una o más de sus entradas son 1 y la compuerta NOT , que se es una compuerta inversora ya que genera un valor de salida que es opuesto al de entrada.(Figura 3).
Figura 3. Compuertas básicas.
MATERIALES Y EQUIPOS:
Los circuitos realizados fueron mediante el simulador Tinkercad. Los materiales usados para elaborar esta práctica fueron los siguientes:-7 protoboard
-3 SPST de conmutadores DIP x 4
-1 SPST de conmutadores DIP x 6
-17 Resistencias de valor 10kΩ
-18 Resistencias de 330Ω
-Cables
-2 Baterias de 4,5V(Construida a partir de pilas de 1,5V)
-17 Resistencias de valor 10kΩ
-18 Resistencias de 330Ω
-Cables
-2 Baterias de 4,5V(Construida a partir de pilas de 1,5V)
-2 Fuentes de voltaje de 5v-18 Diodos Led
-4 C.I: 7400 Cuádruple NAND de dos entradas
-3 C.I: 7402 Cuádruple NOR de dos entradas
-5 C.I: 7404 Inversor séxtuple
-5 C.I: 7408 Cuádruple AND de dos entradas
-5 C.I: 7404 Inversor séxtuple
-5 C.I: 7408 Cuádruple AND de dos entradas
-1 C.I 7410 Triple NAND de tres entradas
-3 C.I: 7432 Cuádruple OR de dos entradas
-3 C.I: 7486 Cuádruple XOR.
-3 C.I: 7486 Cuádruple XOR.
METODOLOGÍA:
En la realización de esta práctica lo primero que se hizo fue identificar el tipo de compuertas y la cantidad que tiene cada circuito planteado. Después de esto se procedió a armar el circuito en Tinkercad. Utilicé la configuración Pull- Down, o sea que tengo una lógica positiva, y cuando el switch este sin presionar se tiene un 0 a la salida y cuando se presiona se tiene un 1.
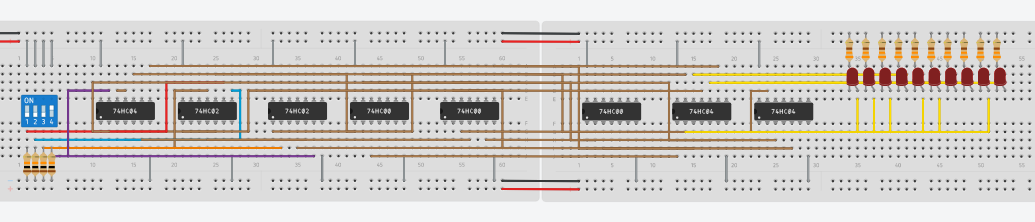
Para el primer circuito se necesitó de tres integrados que son : Integrado 7486 de Puertas XOR, Integrado 7400 de Puertas NAND de 2 entradas y el integrado 7410 de Puertas NAND de 3 entradas. El montaje realizado se puede ver en la Figura 4.
Como podemos ver, el led azul corresponde a una salida, que en este caso es Cout y el led rojo corresponde a la salida S. En el switch la entrada número uno corresponde a A , la número 2 corresponde a B y la número tres a Cin.
En el segundo circuito se compone de las siguientes puertas lógicas: 5 puertas XOR de 2 entradas, 4 puertas NOT, 5 puertas OR de dos entradas y 1 puerta AND de dos entradas. Por ende los integrados usados son : 2 Integrados 7486, 1 integrado 7404, 2 integrados 7432 y 1 integrado 7408. Este circuito tiene 4 entradas y 3 salidas. El montaje realizado se muestra en la Figura 5.
Figura 5. Circuito #2.
Donde el led rojo corresponde a la salida F0, el led azul a la salida F1 y el led verde a la salida F2. Y el orden de las entradas es Z, W X, Y.
Para el tercer circuito propuesto, tenemos las siguientes puertas: 6 puertas NOT, 14 puertas AND, 3 puertas NOR y 4 puertas OR. Por ende los integrados utilizados son: 1 Integrado 7404, 4 integrados 7408, 1 integrado 7402 y 1 integrado 7432. El circuito realizado se muestra en la Figura 6.
Figura 6. Circuito #3.
En este caso tenemos un circuito con 6 entradas, que en montaje se representan en el siguiente orden A2, B2 , A1, B1, A0,B0. Y tenemos 3 salidas que se representan de la siguiente manera: el led verde corresponde a la salida A< B, el led rojo a A>B y el azul representa A=B.
Para el cuarto y último circuito tenemos las siguientes puertas : 16 puertas NOT, 6 puertas NOR y 10 puertas NAND. Y los integrados utilizados fueron: 3 integrados 7404, 3 integrados 7400 y 2 integrados 7402. En la Figura 7 podemos ver el montaje realizado.
Figura 7. Circuito #4.
En el siguiente vídeo se puede observar un breve resumen de la práctica, y se podrá ver la obtención de esta tabla de verdad:
ANÁLISIS DE RESULTADOS:
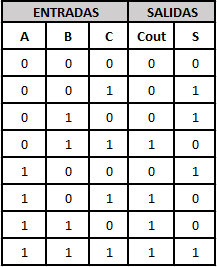
Para el primer circuito tenemos que al momento de realizar la tabla de verdad , tenemos que hay 3 entradas, por ende el número de combinaciones posibles es 2^3, lo que quiere decir que se tienen ocho combinaciones posibles. La tabla de verdad obtenida se pude ver en la Figura 8.
Figura 8. Tabla de verdad circuito #1.
En la tabla de verdad se puede ver que el bit más significativo es el A y el menos significativo es el C.
En el segundo circuito hay 4 entradas, para realizar la tabla de verdad se tiene que el número de combinaciones posibles es 2^4, o sea 16 combinaciones. Entonces, la tabla de verdad obtenida es la que se muestra en la Figura 9.
Figura 9. Tabla de verdad circuito #2.
Para el tercer circuito como tenemos 6 entradas, el número de combinaciones posibles e 2^6, entonces tenemos 64 combinaciones posibles. La tabla de verdad obtenida se encuentra en el link a continuación.
En el último circuito se presentan 4 entradas y 10 salidas, por ende la tabla de verdad tiene 16 posibles combinaciones. En nuestro circuito las entradas van en orden, de la A a la D, y en las salidas el primer led representa la salida "0" y así sucesivamente hasta el led diez que representa la salida "9". La tabla de verdad obtenida se muestra en la Figura 10.
Figura 10. Tabla de verdad circuito #4.
CONCLUSIONES:
-Al finalizar esta práctica se puede concluir que las tablas de verdad de un circuito lógico son demasiado importantes a la hora de implementar algún tipo de circuito. Ya que a través de ellas podemos saber cuál va a ser la respuesta de salida, y conocer el número de combinaciones posibles, teniendo en cuenta las entradas que tenga el circuito.
-También fue interesante realizar esta práctica, ya que uno puede darse cuenta de como funcionan estos circuitos y comprender que una función lógica nos permite que una o más salidas tengan cierto valor dependiendo de un valor determinado en las entradas. Y de esta manera tener algunas ideas de los comportamientos de las puertas lógicas que serán útiles a la hora de realizar un diseño propuesto.
FUENTES:
- Floyd, T. (2006). Fundamentos de Sistemas Digitales (9.a ed., Vol. 1). Madrid, España: PEARSON EDUCACIÓN.-Bosque , G. (2016). Principios de Diseño de Sistemas Digitales (1.1 ed., Vol. 1). Recuperado de https://web-argitalpena.adm.ehu.es/pdf/UCWEB142021.pdf
-Brown, S. (2006). Fundamentos de Lógica Digital con Diseño VHDL (Segunda ed., Vol. 1). México, D. F., México: McGraw-Hill Companies.