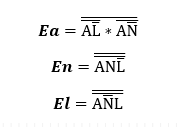Taller parciales anteriores.
https://circuitverse.org/users/25319/projects/110743
https://circuitverse.org/users/25319/projects/112703
-Se quiere implementar un sistema con dos luces de alarma (diodos LED) y tres sensores (entradas digitales). Llamaremos A y B a las luces de alarma, y x2, x1 y x0 a los sensores digitales. El sistema deberá funcionar de la siguiente manera:
* La alarma A se dispara si se recibe señal del sensor x2 exclusivamente.
* La alarma B se dispara si se recibe señal del sensor x0 exclusivamente.
* Las dos alarmas se disparan si se recibe señal de al menos dos sensores cualesquiera.
a) Realizar la tabla de verdad del sistema de alarma (tabla de verdad).
b) Realizar una implementación con puertas AND-OR.
Para realizar el
circuito con puertas AND-OR, realizamos los mapas de Karnaugh para las alarmas
A y B, entonces:
Y el circuito obtenido es:
c) Realizar una implementación con puertas NAND.
Y con compuertas NAND:
DISEÑO SISTEMAS COMBINACIONALES:
-Una máquina expendedora automática proporciona
productos con diversos precios: botella de agua 0,50 €, lata de refresco 1,00
€, paquete de galletas 1,50 € y caja de bombones 2,00 €. Sólo admite una moneda
de 0,50 €, 1,00 € ó 2,00 € para adquirir el producto y sólo devuelve cambio de
1 moneda, caso de que tuviera que devolver cambio. Habrá casos en los que, al
no poder proporcionar el cambio correcto, devolverá la moneda introducida, sin
proporcionar el producto.
Tenemos que los productos son:
-Botella
de agua
-Lata
de refresco
-Paquete
de Galletas
-Caja
de bombones
Y
las monedas que se admiten son:
-0.50
-1.00
-2.00
Entonces las entradas están dadas por los productos y las monedas que se admiten. Los nombres asignados a cada entrada son los siguientes:
-Monedas:
A, B
-Productos:
Pro1, Pro2
Y codificando estas entradas se tiene:
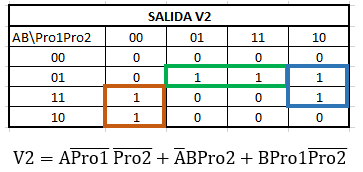
Para las salidas se tiene que están dadas por las vueltas o las monedas que se devuelven, y por el producto adquirido, entonces los nombres asignados son:
-Monedas
devueltas: V1, V2
-Producto
adquirido: P. Adq
Y estas salidas codificadas son:
2) Deducir la tabla de verdad que define las relaciones entre las variables de entrada y de salida.
3) Simplificar las funciones representadas en la tabla de verdad.
4) Obtener el circuito a partir de las funciones simplificadas.
DISEÑO CON SUMADORES:
-Diseñe un multiplicador binario que multiplique un
numero de 4 bits B = b3 b2 b1 b0 por un numero de 3 bits A = a2 a1 a0 para
formar el producto C = c6 c5 c4 c3 c2 c1 c0. Esto puede lograrse con 12
compuertas y dos sumadores de 4 bits.
Primero analizamos como es la multiplicación binaria,
entonces:
Entonces según lo anterior las 12 compuertas que necesitamos son compuertas AND de dos entradas y los dos sumadores correspondientes. Por ende, el circuito diseñado es el siguiente:
DISEÑO COMBINACIONAL:
-Usando Mapas de Karnaugh para las siguientes funciones:
(a) Encuentre la solución mínima de cada función
(b) Implemente la solución mínima de cada función, usando la menor cantidad posible de circuitos integrados.
(a) Encuentre la solución mínima de cada función
(b) Implemente la solución mínima de cada función, usando la menor cantidad posible de circuitos integrados.
Para implementar la solución, utilicé 3 integrados, que corresponden a 1 integrado 7404(4/6), 1 integrado 7400 (4/4), y 1 integrado 7410(3/3).
COMPUERTAS UNIVERSAL NAND:
-Se desean controlar dos bombas B1 y B2 en función de la cantidad de agua en un depósito. Los sensores B (nivel bajo de agua) y A (nivel alto de agua) entregan un uno lógico cuando el agua supera dicho nivel. Los sensores TB1 y TB2 indican mediante un uno si la temperatura de las bombas B1 y B2 ha superado el límite de funcionamiento. Si el nivel se encuentra:
- por debajo de B se deben activar las dos bombas;
- por encima de B pero por debajo de A se debe activar
una bomba, preferiblemente B1 (teniendoen cuenta su temperatura);
- por encima de A se deben desactivar B1 y B2;
- si la temperatura del motor superara el límite, éste
debería pararse.
Cualquier situación anómala en los valores de los sensores conllevará la parada de ambas bombas por seguridad.
Se plantea la tabla de verdad del comportamiento de las bombas, teniendo en cuenta los sensores mencionados, entonces:
Y con estas ecuaciones se realizó el siguiente circuito usando solo compuertas NAND:
DISEÑO SISTEMAS COMBINACIONALES:
Un circuito tiene tres sensores lumínicos puestos a
diferentes alturas, alto, mediano y bajo, SA, SM y SB. Si un diamante es grande
interfiere las tres señales lumínicas, si es mediano, dos (SM y SB), si es pequeño,
una (SB) y si es enano, ninguna. El sensor de peso en quilates (SP) que se pone
a 1 si supera los tres quilates, y a 0 en caso contrario. Las condiciones son:
- Un diamante grande (G) o mediano (M) debe pesar al
menos 3 quilates, si no, se rechaza (R).
- Si es pequeño, nunca debe pesar más de 3 quilates,
en caso contrario es rechazado (R).
- Los diamantes enanos se rechazan (R).
- Las condiciones irreales, se consideran imposibles.
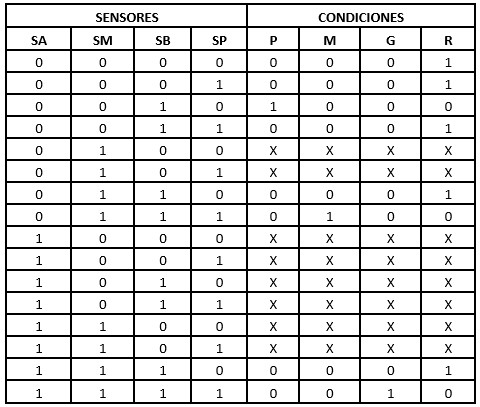
Primero se plantea la tabla de verdad, teniendo en
cuenta las condiciones planteadas, entonces:
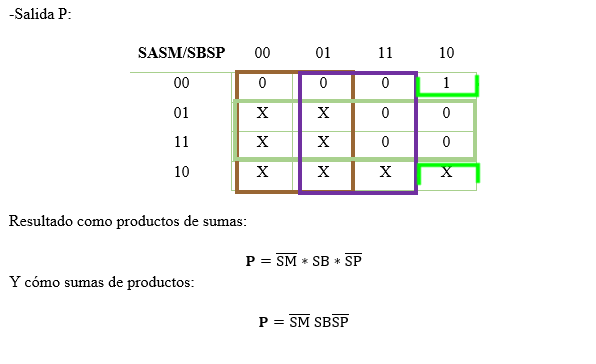
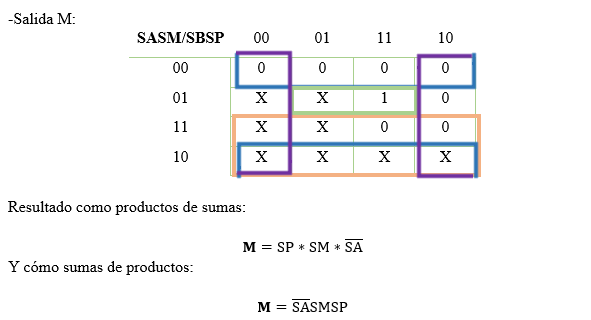
Con la tabla realizada podemos analizar los
mintérminos y maxtérminos de cada salida, y como resultado tenemos:
Y
las combinaciones irreales corresponderían:
Entonces realizando la tabla de verdad con estas combinaciones y con las combinaciones irreales, tenemos:
Entonces con estas expresiones reducidas se realizo el circuito correspondiente :
DISEÑO CON DECODIFICADORES:
-Diseñar un bloque decodificador de cinco variables
(32 salidas) basándose en el decodificador 4:16 y los circuitos auxiliares que
sean necesarios.
Primeramente para construir el decodificador de 4 a 16, lo hice a partir de 5 decodificadores 2 a 4 y con un circuito enable. Entonces para los decodificadores 2 a 4 se tiene:
Entonces a partir de este decodificador se realizo el 4 a 16, de la siguiente manera:
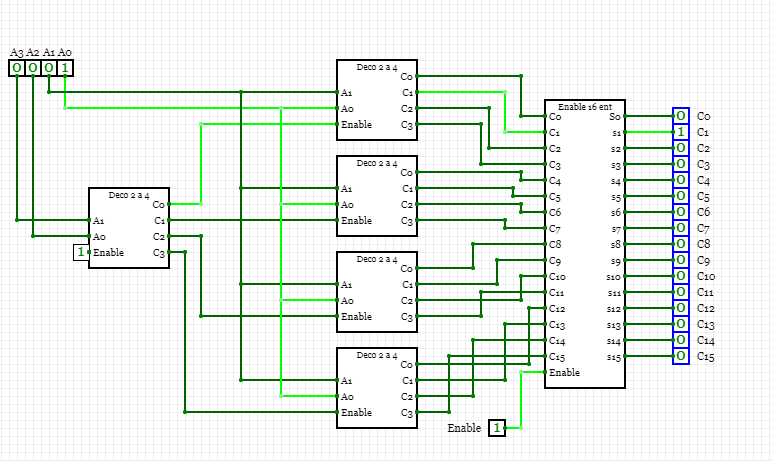
Y ya con el decodificador 4 a 16, se realizo el 5 a 32,de la siguiente manera:
-Diseñar un sistema decodificador de cuatro variables de entrada (2^4=16 salidas) a partir de decodificadores de tres variables de entrada (2^3=8 salidas).
Para construir el decodificador de 3 a 8, lo hice a partir de 2 decodificadores 2 a 4, mostrado anteriormente, y un circuito enable. Entonces como resultado se obtuvo:
Y con este decodificador ya realizado, lo utilice para hace el decodificador 4 a 16, y se obtuvo:
-Diseñar un sistema decodificador de seis variables de
entrada ( 2^6=64 salidas) a partir de decodificadores de cuatro variables de
entrada (2^4=16 salidas).
Entonces partiendo del decodificador 4 a 16 realizado anteriormente se necesitaron 4 decodificadores y 1 decodificador 2 a 4, y el montaje es el siguiente:
DISEÑO CON MULTIPLEXORES:
-Usando un multiplexor diseñe un circuito que detecte
los siete primeros números de la secuencia de Fibonacci. Esta secuencia se
define recursivamente: F (1) = F (2) = 1 Y F (n) = f (n-1) + f (n-2), para
n>2.
Tenemos que para este problema , la secuencia de Fibonacci esta dada por:
F(1)= 1, 1, 2, 3, 5, 8, 13, 21, 34.... pero como solo nos piden los 7 primeros términos nos damos cuenta que necesitamos una tabla de verdad de 32 combinaciones, o sea 5 entradas. Entonces la tabla de verdad correspondiente teniendo en cuenta los términos de la función es:
Ahora para saber que Mux utilizar aplicamos que el Mux tiene que ser de 2^(n-1) a 1, donde n es el número de entradas. Entonces según esto el Mux que debemos usar es de 2^4 a 1, o lo que quiere decir de 16 a 1. En donde los selectores, son las entradas más significativas.
Entonces como se observa en la tabla de verdad en la columna de la derecha están las entradas del Mux. Entonces para saber las entradas del Mux, tenemos que comparar la entrada E, con la función de salida, y se analiza el comportamiento que se tiene, esto se ve reflejado en la última columna de la tabla.
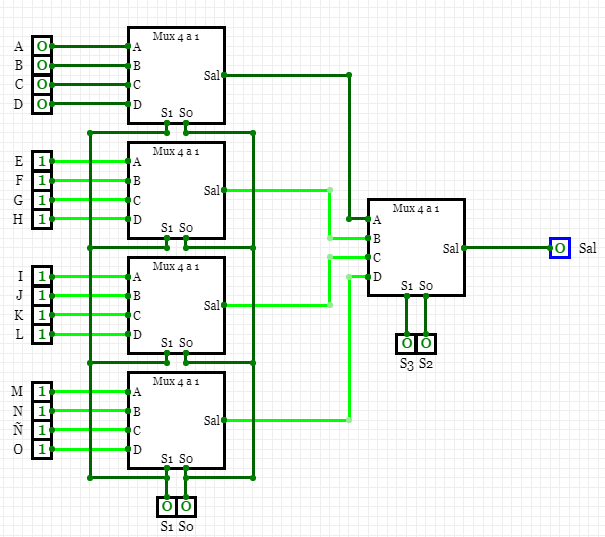
En el diseño del Mux se realizó a partir de 5 Mux 4 a 1, de la siguiente manera:
Ahora implementando los valores de la tabla de verdad en el Mux, para obtener la función deseada se tiene:
COMPUERTAS UNIVERSAL NAND:
-El sistema nervioso humano, incluyendo al cerebro, está hecho de billones de células especializadas llamadas neuronas. Cada neurona posee sinapsis (nodos, puntos de conexión con otras neuronas) que pueden ser de dos tipos: (1) excitatorias e (2) inhibitorias. Cada neurona tiene una sola terminal de salida, (la cual se denomina axón), y transmite por ella una señal [1] cuando el número de sinapsis excitatorias con entradas [1], excede al número de sinapsis inhibitorias con entrada [1] por al menos el número N (umbral de la neurona). Determine la función de la salida F(A, B, C, D, E) en el axón de la neurona, dadas las siguientes condiciones:
Tenemos que, para desarrollar este problema, lo primero es que hay que tener claro que de sinopsis de excitación se tiene a A, B, C y de sinopsis de inhibición se tiene a D, E, y que solo se tiene una terminal de salida (F). Ahora teniendo en cuenta las condiciones dadas en el enunciado del problema, para tener 1, 0 y salidas “no importa” se procedió a construir y llenar la respectiva tabla de verdad. Como son 5 entradas, la tabla tiene 32 posibles combinaciones.
Ahora, analizando la tabla de verdad, podemos
obtener los mintérminos y maxtérminos. Y para la elaboración del Mapa de
Karnaugh también se tendrán en cuenta los términos no importa. Entonces los
mintérminos y maxtérminos son:
Ahora colocando lo anterior en el Mapa de Karnaugh se tiene:
Como resultado se obtuvo el siguiente circuito:
DISEÑO SISTEMAS COMBINACIONALES:
-Implementar un circuito con 5 variables de entrada con decodificadores de 4 entradas que realice la siguiente función: S = f(A, B, C, D, E) = m1+m2+m3+m7+m12+m31
Empiezo desarrollando la tabla de verdad correspondiente, teniendo en cuenta las entradas y los miniterms que se requieren mostrar, entonces:
Ahora como nos están diciendo que el decodificador tiene que tener 4 entradas, entonces necesitamos un decodificador de 4 a 16. Para desarrollar este decodificador, me base de 2 decodificadores 3 a 8 y con un circuito enable. Entonces el decodificador quedó de la siguiente manera:
Ahora implementando la función que nos están pidiendo, teniendo en cuenta los mintérminos, y como se comporta el decodificador al tener ciertas combinaciones en las entradas, utilicé dos decodificadores 4 a 16 y 3 compuertas OR (2 de 3 entradas y 1 de 2 entradas) se realizó el siguiente circuito:
Y el circuito anterior,muestra los mintérminos requeridos en el problema.
-Implementar un circuito con 5 variables de entrada con multiplexadores de 8 entradas que realice la siguiente función: S = f(A, B, C, D, E) = m1+m2+m3+m6+m9+m11+m19
Lo primero a realizar es la tabla de verdad, teniendo en cuenta los mintérminos que se nos requieren, y las entradas que nos están dando. Entonces tenemos:
Ahora teniendo en cuenta las entradas del Mux que nos están pidiendo, necesitamos utilizar un mux de 8 a 1 , que cuenta con 3 selectores. Entonces realizando el análisis para mostrar la función con el Mux, tenemos que en este caso estamos implementando un Mux de 2^n-2, donde n es el número de entradas, entonces los 3 selectores serán las 3 entradas más significativas del circuito, que en este caso son A, B, y C. Y las entradas D y E serán comparadas con la función de salida. Con esto tenemos que se debe tener a las entradas del Mux. En la tabla de verdad anterior, se puede observar que en la parte izquierda se encuentran las entradas del Mux, y en la parte derecha se encuentra la ecuación obtenida al realizar la comparación.
Entonces teniendo esto claro, realice el circuito correspondiente a las entradas del Mux, y se obtuvo:
-Deducir la
expresión algebraica en minterms del siguiente circuito:
Teniendo en cuenta las salidas del decodificador en Q0, Q2,Q3,Q6 y las compuertas que se manejan en el circuito, se tiene que la expresión de salida es:
Y realizando la tabla de verdad se tiene que:
Entonces la expresión de salida expresada en mintérminos es:
DISEÑO CON COMPUERTAS UNIVERSAL:
- La apertura y cierre del tejado de un
invernadero de flores de decoración depende del estado de 4 sensores que
controlan la temperatura (T), la velocidad del viento (V), la presión atmosférica
(P) y la humedad del ambiente (H). El cierre se producirá de manera automática
cuando se active un motor controlado por la señal de salida del circuito de
control que queremos diseñar. Dicha señal de salida pondrá en funcionamiento el
motor siempre y cuando se produzca alguna de las siguientes condiciones
climatológicas: T ACTIVO La temperatura ambiente supera los 30o C; V ACTIVO
Velocidad del viento superior a los 50 → → Km/h; H ACTIVO Humedad inferior al
40 %.
a) Calcule la función
lógica de salida del circuito que activa el motor de cierre.
Para obtener la función de salida, realicé la tabla de verdad, teniendo en cuenta las especificaciones dadas en el problema. Entonces:
b) Simplifique la función
lógica mediante el método de Karnaugh.
Ahora utilizando los mapas de Karnaugh para simplificar la expresión obtenida, se tiene:
c) Implemente el circuito
con puertas lógicas universales NAND ó NOR.
Implementando el circuito con compuertas NAND :
DISEÑO CON MULTIPLEXOR:
-Se pretende diseñar un
circuito combinacional que detecte los meses del año que tengan más de 30 días.
Para ello el circuito dispone de 4 entradas (a, b, c y d) para codificar en
binario el mes en cuestión, empezando por 0001 (enero). Se pide:
a) Obtener la tabla de
verdad.
Primeramente se codificaron los meses desde 0001 que corresponde a enero, hasta 1100 que corresponde a diciembre, como se muestra en el enunciado, ya con esto, se realizo la tabla de verdad.
Desarrollando la tabla de verdad según las indicaciones se tiene:
b) Obtener la ecuación
lógica correspondiente a su primera forma canónica.
La función canónica de salida obtenida de los mintérminos es:
c) Simplificar la
ecuación.
Para simplificar la ecuación lo realice mediante Mapas de Karnaugh de la siguiente manera:
d) Diseñar el circuito
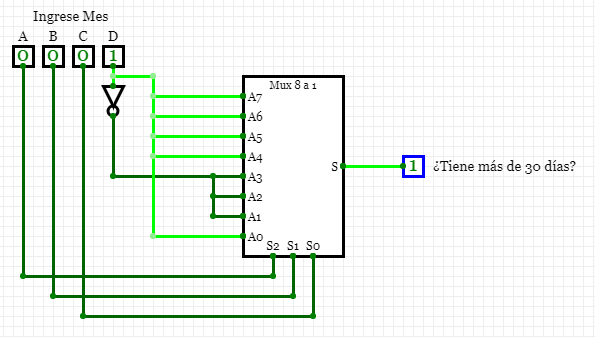
completo con multiplexor.
Para realizar el diseño con el multiplexor, se tuvo en cuenta que el tamaño del Mux es de 2^n-1 a 1, donde n es el número entradas. Por ende el Mux utilizado es de 8 a 1. Y para obtener las entradas del Mux se realizo comparando el valor de D con la función de salida. También tenemos 3 selectores, que son utilizados como las entradas más significativas del circuito. Entonces se obtuvo:
DISEÑO CON COMPUERTAS DE DOS ENTRADAS:
-Se pretende construir un circuito combinacional de control de paro automático del motor de un ascensor de un edificio. El funcionamiento del motor depende de 4 variables. En primer lugar, de que la puerta del ascensor esté abierta o cerrada (A); en segundo lugar, del peso de las personas que suben al ascensor (P); en tercer lugar, de que alguna de las persona haya pulsado los pulsadores de las distintas plantas (B); y por último, de la temperatura del motor (T). El motor se parará automáticamente siempre que la puerta del ascensor esté abierta, o bien se sobrepase el peso máximo, que es de 800 kg. T→ Temperatura; P→ peso; A → puerta; B→pulsador de planta.
a) Calcule la función
lógica de salida de paro automático del motor del ascensor.
Para obtener la función lógica de salida se realizó la tabla de verdad, teniendo en cuenta las condiciones que se nos dan:
Entonces la función de salida expresada por Maxtérminos es:
b) Simplifique la función
lógica mediante el método de Karnaugh.
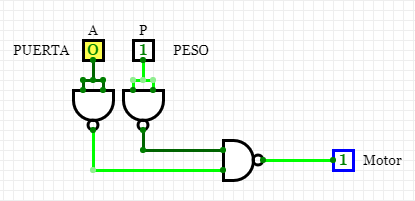
c) Implemente el circuito
con puertas lógicas universales NAND.
SISTEMAS DE NUMERACIÓN:
Realice la conversión de los siguientes números al sistema de numeración correspondiente en cada casilla:
ANÁLISIS DE SISTEMAS COMBINACIONALES:
a) Encuentre la tabla de verdad para el sistema digital:
La tabla de verdad para este circuito corresponde a:
b) Encuentre una
expresión algebraica en forma de suma de productos:
La ecuación encontrada en forma de suma de productos es:
c) Aplique algebra de
Boole para reducir la anterior expresión algebraica:
Aplicando Algebra de Boole
tenemos:
d) Implemente el mismo
sistema digital usando únicamente compuertas NAND de 2 entradas.
Se tiene que para tener el circuito en compuertas NAND, hacemos lo siguiente con la ecuación de salida:
Usando Mapas de Karnaugh para las siguientes funciones:
(a) Encuentre la
solución mínima de cada función:
(b) Implemente la
solución mínima de cada función, usando la menor cantidad posible de circuitos
integrados.
Implementando la función anterior utilice: 1 integrado 7404(6/6), 1 integrado 7410(3/3), y un integrado 7400(4/4). Para un total de 3 integrados:
(a) Encuentre la solución mínima de cada función:
(b) Implemente la
solución mínima de cada función, usando la menor cantidad posible de circuitos
integrados.
Para implementar la solución mínima de esta función, utilice 1 integrado 7404 (5/6), 1 integrado 7410(3/3), y 1 integrado 74000(4/4). Para un total de 3 integrados.
Una máquina de refrescos
tiene y tres pulsadores a, n, y l (a para el agua, n para la naranja l para el
limón), y tres depósitos con agua, naranja y limón. Cada uno de los depósitos
está controlado por una electroválvula: Ea para el depósito del agua, En para
el depósito de la naranja y El para el depósito del limón. Se desea diseñar el
automatismo de control de la máquina de forma que se cumplan las siguientes condiciones:
a. La máquina puede dar
agua, agua con limón y agua con naranja, pero nunca naranja o limón solos o
mezclados.
b. La electroválvula de
cada uno de los depósitos se activará por medio de su correspondiente pulsador
y siempre que se cumplan las condiciones establecidas en el problema.
c. La desconexión de las
electroválvulas se producirá cuando el vaso de refresco se haya llenado, al
actuar, debido a su peso, sobre un pulsador cuando el vaso este lleno
Lo primero a realizar en este diseño es la tabla de verdad, teniendo en cuenta las condiciones especificadas, entonces la tabla de verdad queda de esta manera:
Ahora teniendo en cuenta las salidas, se obtiene cada expresión con los Mapas de Karnaugh, entonces:
Para implementar el circuito con solo compuertas universales, se hace los siguiente:
Y el circuito realizado es:
Como se observa en la anterior imagen, las 6 compuertas NAND de la derecha, corresponden a un circuito que me habilita o me des-habilita las electro-válvulas, dependiendo del peso que se tenga. Cuando el vaso se llene, el pulsador se activa y des-habilita las electro-válvulas.
DISEÑO CON MULTIPLEXOR:
Un sistema automatizado
de riego nos indica el nivel de humedad del suelo mediante dos sensores A y B.
Cuando no es necesario el riego ambos sensores están a 0. Los riegos se
realizarán siempre que alguno de los sensores, A o B, esté activo,
preferentemente por la noche, salvo en el caso de sequedad extrema que podrán
ser a cualquier hora del día. Cuando la sequedad es extrema ambos sensores, A y
B, se ponen a 1. El sistema dispone de un sensor de luz C que se activa al
oscurecer. Por otra parte, el suministro de agua procede de un depósito que nos
manda una señal activa D cuando no tiene suficiente líquido para el riego y por
tanto no se puede realizar.
Diseñar el circuito que
gobierne la válvula que abre el paso de agua.
a) Obtener la tabla de
verdad.
La tabla de verdad para este circuito según las condiciones , es la siguiente:
b) Obtener la ecuación
lógica correspondiente a su primera forma canónica.
c) Simplificar la
ecuación.
Para simplificar la ecuación lo haré mediante Mapas de Karnaugh, con lo que se obtuvo:
d) Diseñar el circuito completo con multiplexor.
Para diseñar el circuito con un Multiplexor, lo haré teniendo en cuenta que el tamaño del Mux va a ser de 2^n-1 a 1, teniendo en cuenta que n es el número de entradas que tengo. Entonces el Mux es de 8 a 1, y los 3 selectores serían las entradas más significativas, que en este caso son A,B Y C. Con esto claro, ahora miramos que va en las entradas del Mux, por ende se analiza la tabla de verdad y la entrada D, se compara con la salida, y con esto tenemos lo que va en la entrada del Mux, de la siguiente manera:
Entonces el circuito diseñado es el siguiente:
Al depósito de la
figura acceden 4 canalizaciones cuyos caudales se muestran en la figura. Del
depósito salen otras cuatro canalizaciones cuyos caudales se muestran también.
Teniendo en cuenta que a la entrada solo puede haber dos canalizaciones
abiertas al mismo tiempo, diseñar un circuito que gobierne las electroválvulas
de salida para que, dependiendo de las electroválvulas de entrada que estén
abiertas, el caudal de entrada sea igual al de salida.
Primeramente se desarrolla la tabla de verdad, de acuerdo a las condiciones que se dan,y teniendo en cuenta que en el enunciado solo nos mencionan que a la entrada solo puede haber dos canalizaciones abiertas al mismo tiempo, pero en la salida no se tiene esta condición, entonces:
Entonces para obtener la ecuación de cada salida, se realiza a partir de los mapas de karnaugh, de la siguiente manera:
Ahora implementado el circuito con las ecuaciones obtenidas, y utilizando solo compuertas de 2 entradas, se tiene:
Entonces de una mejor manera, el circuito queda de esta manera: