Práctica #9.
Nombre de la práctica : Universalidad de las compuertas NOR Y NAND
Nombre: David Santiago Martínez Molina
Código: 20181005164
Asignatura: Fundamentos de circuitos digitales
Programa : Ingeniería Electrónica
Docente : César Andrey Perdomo Charry
INTRODUCCIÓN:
A lo largo de este informe se mostrará el desarrollo de la práctica #9. Para esta práctica se nos requiere implementar un sumador/restador de 6 bits, utilizando multiplexores, y compuertas NAND y NOR. En el desarrollo de esta práctica fue necesario comprender como se construye cualquier circuito con compuertas NAND y NOR.
La universalidad de la puerta NAND significa que puede utilizarse como un inversor y que pueden emplearse combinaciones de la puerta NAND para implementar las operaciones AND, OR y NOR. Del mismo modo, la puerta NOR se puede utilizar para implementar el inversor (NOT) y las operaciones AND, OR y NAND.
Propiedad universal puertas NOR:
La puerta NOR se puede utilizar para generar las funciones NOT, AND, OR y NAND. Un circuito NOT, o inversor, puede obtenerse a partir de una puerta NOR conectando todas sus entradas juntas para tener una única puerta, con una puerta de 2 entradas. También puede obtenerse una puerta OR a partir de puertas NOR. Un puerta AND puede construirse utilizando puertas NOR como muestra la Figura 1.
Figura 1.Universalidad puerta NOR.
Propiedad universal puertas NAND:
La puerta NAND es una puerta universal porque puede utilizarse para generar las funciones NOT, AND, OR y NOR. Se puede obtener un inversor a partir de una puerta NAND conectando juntas todas las entradas, dando lugar a una única entrada, con una puerta de 2 entradas. La operación AND se puede generar utilizando sólo puertas NAND, La operación OR se puede obtener con varias puertas NAND, Por último, la operación NOR se obtiene como se indica en la figura 2.
Figura 2.Universalidad puerta NAND.
Sumador Completo:
Los sumadores son muy importantes no solamente en las computadoras, sino en muchos tipos de sistemas digitales en los que se procesan datos numéricos. Comprender el funcionamiento de un sumador básico es fundamental en el estudio de los sistemas digitales.
El sumador completo supone un circuito un poco más complejo. A diferencia del semi-sumador, nos permite incluir en la suma de dos bits el acarreo de una suma anterior a través de una entrada que se llama Cin, con lo que ya podremos realizar cualesquiera sumas.
Un sumador acepta dos bits de entrada y un acarreo de entrada, y genera una salida de suma y un acarreo de salida. El sumador completo tiene que sumar dos bits de entrada y un acarreo de entrada. Del semi-sumador sabemos que la suma de los bits de entrada A y B es la operación OR-exclusiva de esas dos variables, A ⊕ B. Para sumar el acarreo de entrada (Cin) a los bits de entrada, hay que aplicar de nuevo la operación OR-exclusiva, obteniéndose la siguiente ecuación para la salida de suma del sumador completo:
El símbolo lógico de un sumador completo corresponde a :
MATERIALES Y EQUIPOS:
En el Mux 16 a 1:
-5 Mux 4 a 1(27 puertas NAND, 6 entradas, 1 salida)
Para el sumador de 2 bits:
-3 Mux 16 a 1
-5 entradas
-3 salidas
-1 puerta NOT
Para el sumador de 6 bits:
-3 sumadores de 2 bits.
Para el comparador de 2 bits:
-30 puertas NOR de dos entradas.
-4 entradas.
-3 salidas.
Para el comparador de 6 bits:
-1 comparador de 4 bits(a partir de 2 de dos bits)
-1 comparador de 2 bits
-Circuito adicional(17 puertas NOR de 2 entradas, 6 entradas, 2 salidas)
Para realizar el complemento a 1:
-12 puertas XOR de 2 entradas
-12 entradas
-12 salidas.
Para el sumador/restador de 6 bits:
-13 entradas
-1 Sumador de 6 bits
-1 Circuito complemento a 1
-1 Comparador 6 bits
-2 Puertas AND y 1 NOT(Para realizar el complemento dependiendo el caso)
-2 Puertas AND de 2 entradas ( Para el signo y corrección de la resta por complemento)
-8 salidas ( 1 de signo, 7 de resultado)
METODOLOGÍA:
En el desarrollo de esta práctica lo primero que se realizo fue el Mux 4 a 1, para construir el Mux 16 a 1. Entonces para desarrollar el Mux 4 a 1 solo con compuertas NAND, se tiene que la tabla de verdad reducida esta dada por: ( teniendo en cuenta que son 2 selectores)
Ahora teniendo en cuenta la tabla de verdad reducida, se realizó el Mapa de Karnaugh de 6 variables de entrada, entonces queda de la siguiente manera:
Y se obtuvo la siguiente ecuación agrupando como se ve en el Mapa anterior:
Pero como necesitamos implementar el circuito con solo compuertas NAND, entonces realizamos las leyes de De Morgan a la ecuación de salida obtenida, y se obtuvo:
Y el circuito realizado es el siguiente:
Ya con el Mux 4 a 1 realizado, ahora se construye el Mux 16 a 1, a partir de 5 Mux 4 a 1, conectando los selectores de la siguiente manera:
Entonces lo siguiente a realizar es el sumador completo de 2 bits, a partir de 3 Mux 16 a 1. Para realizar esto, primero se plantea la tabla de verdad de un sumador completo, teniendo en cuanta las características que tiene este sumador. Luego de que se tiene la tabla, se plantea de que manera el Mux de 16 a 1, me va a implementar las funciones de salida del sumador, entonces teniendo en cuenta que el sumador es de 2^n-1 a 1, donde n es el numero de entradas correspondientes, o sea el sumador es de 2^4 a 1. Lo que se realiza es comparar la entrada menos significativa, que en este caso es Cin, con el comportamiento de las salidas que tenemos. Esto quiere decir, que necesitaremos 3 Mux 16 a 1, ya que tenemos 3 salidas, y cada Mux me va a implementar una salida. Entonces el primer Mux corresponde a la función de salida Cout, y por ende las entradas de este Mux son el resultado de comparar Cin con Cout. Para el segundo Mux se correspondería a la función de salida S1, y se compara de la misma manera con Cin. Y para el último Mux, se tiene que es la función de salida S0, y las entradas del Mux se obtendrían comparando S0 con Cin.
Ahora como el Mux es de 16 a 1, tenemos que hay 4 selectores. Dichos selectores serán las entradas más significativas de nuestro sumador o sea A1,A0,B1 Y B0, y los selectores de cada Mux van conectados mutuamente a estas 4 entradas.
Entonces la tabla de verdad obtenida, teniendo en cuenta lo mencionado para implementar las salidas con el Mux es:
Entonces siguiendo la anterior tabla de verdad, el circuito realizado es:
En el siguiente vídeo se puede observar la metodología utilizada y una explicación del laboratorio realizado:
LINK DEL VÍDEO : https://youtu.be/fc2V9GqjpOs
ANÁLISIS DE RESULTADOS:
Teniendo en cuenta el sumador de 2 bits realizado anteriormente construí el sumador de 6 bits conectando los sumadores de 2 bits de la siguiente manera:
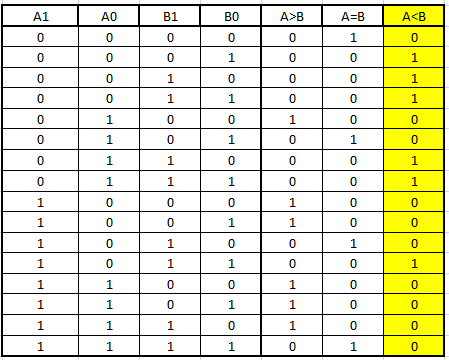
Ahora para realizar el sumador/restador, hay que tener en cuenta, que la resta se debe hacer por complemento a 2, además que no se puede olvidar la corrección cuando el número A es menor que el número B. Entonces para verificar si el número A es menor que B, se necesita realizar un comparador de 6 Bits, y dicho comparador tiene que estar construido únicamente por compuertas NOR. Para realizar este comparador de 6 bits, se empieza haciendo un comparador de 2 bits. Entonces la tabla de verdad de este comparador corresponde a:
Y a partir de esta tabla de verdad se obtienen las funciones de salida mediante los Mapas de Karnaugh, de la siguiente manera:
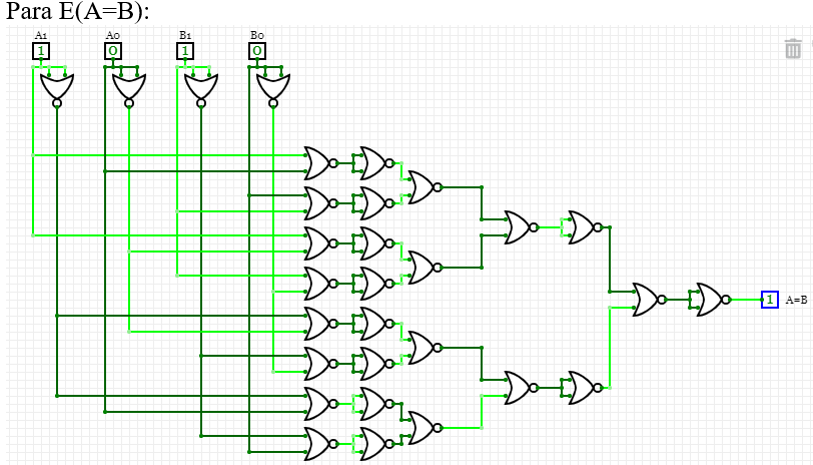
Ya con las salidas obtenidas, se realiza el circuito, utilizando únicamente compuertas NOR de dos entradas, entonces el circuito queda de la siguiente manera:
Ahora utilizando 2 comparadores de 2 bits, se realiza un comparador de 4 bits de la siguiente manera:
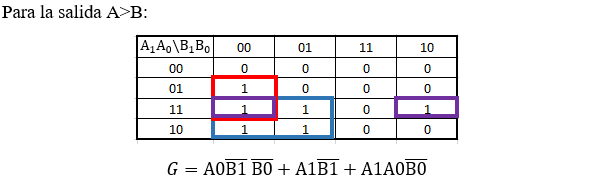
El circuito que se observa en la anterior figura, denominado "Circuito con NOR", se realizo para obtener las 3 salidas que se necesitan en el comparador, y se hizo a partir de los Mapas de Karnaugh, teniendo en cuenta las condiciones que no importan o que nunca se deben dar a las salidas de los comparadores, entonces para la salidas G (A>B), E(A=B), L(A<B), se tiene:
Entonces implementando las ecuaciones de salida en solo compuertas NOR, se tiene:
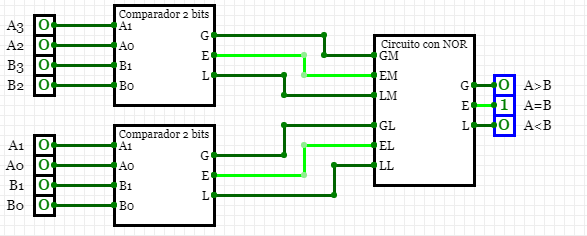
Y para construir el comparador de 6 bits, se utiliza un comparador de 4 bits y uno de 2 bits y para obtener las salidas que necesitamos utilizamos el circuito anterior, entonces:
Ya con el comparador hecho entonces solo queda realizar el restador. Para hacer el restador se tiene que tener en cuenta que la resta se va a realizar a través del complemento a 2, entonces se tienen dos casos, un caso es cuando A>B, y la resta se realiza aplicando el complemento a 2 al número B, y este se suma al número A. El otro caso es cuando A< B, y para solucionar esta resta se tiene que hacer el complemento a 2 del número A y se suma al número B, o también se puede hacer aplicando el complemento a 2 al número B (como ocurre cuando A>B) y la suma obtenida se vuelve a complementar y este es el resultado final.
Para este laboratorio aplique la opción de complementar A y B, dependiendo de si A<B, como mencione anteriormente. Entonces hay que recordar que el complemento a 2 se realiza primero aplicando el complemento a 1 y sumando 1 a este resultado. Este 1 que se suma, viene de la entrada Cin, que es la que me va a permitir tener un sumador o un restador. Y para aplicar el complemento a 1 lo hice utilizando compuertas XOR de dos entradas, en los números A y B, y colocando una entrada común para cada número, de la siguiente manera:
Como se ve en la anterior imagen, las entradas que están a la derecha, que se denominan A y B, son las que me permiten realizar el complemento a 1. Entonces estas entradas de penden, de si se tiene una suma o una resta, y de la salida que se tenga en el comparador, o sea si A< B. Con esto claro, realice la siguiente tabla de verdad, donde se analiza para que casos se debe complementar A o B, según si es suma o resta y si A<B, entonces:
Como se observa en la tabla de verdad, solo se va a complementar A, cuando se tiene una resta y A<B. Y solo se complementa B, cuando se tiene una resta y la salida del comparador es 0(o sea A=B o A>B). Entonces aplicando esto a un circuito, correspondería a 2 compuertas AND y una puerta negadora.
Ya con el restador implementado, solo quedaría mostrar el signo y la corrección al aplicar el complemento a 2. Hay que tener en cuenta que cuando se realiza una resta por complemento a 2 siempre se genera un bit de más y este se descarta, entonces para corregir este bit y para mostrar el signo, realice la siguiente tabla de verdad:
Entonces implementando todo lo anterior finalmente el circuito SUMADOR/ RESTADOR de 6 bits que se obtiene es el siguiente:
En el anterior circuito, se pueden observar todos los circuitos desarrollados y se puede comprobar el funcionamiento del sumador/restador, en la pestaña que se denomina SUMADOR/RESTADOR 6 BITS.
CONCLUSIONES:
-Comprobando el funcionamiento del sumador/restador se puede observar que funciona correctamente, y cumple con los requerimientos pedidos.
-Se pudo enfatizar más en como implementar cualquier circuito con compuertas NAND y NOR, y aplicarlos en un Mux.
FUENTES:
- Floyd, T. (2006). Fundamentos de Sistemas Digitales (9.a ed., Vol. 1). Madrid, España: PEARSON EDUCACIÓN.
-Brown, S. (2006). Fundamentos de Lógica Digital con Diseño VHDL (Segunda ed., Vol. 1). México, D. F., México: McGraw-Hill Companies.